FERMAT PUNKTEN
Uppgift
Fermat formulerade 1643/44 följande minimumproblem:
Bestäm den punkt P i triangeln ABC för vilken summan av avstånden från P till triangelns tre hörnpunkt (dvs.|PA|+|PB|+|PC|) är minimal. Denna punkt P kallas därför ’Fermat’-punkt.
Toricelli hittade flera lösningar (bl.a. en med en ellips), sedan bidrog flera matematiker med lösningar: Viviani, Cavalieri, Steiner mm., P kallas även Fermat-Toricelli-Steiner-punkt. (Pierre de Fermat, 1601-1665; Evangelista Toricelli, 1608-1647; Jakob Steiner, 1796-1863).
I denna uppgift skall du ge en lösning av Fermats minimumproblem som ger enkla konstruktioner av Fermatpunkten och upptäcka flera förbluffande egenskaper i samband med den:
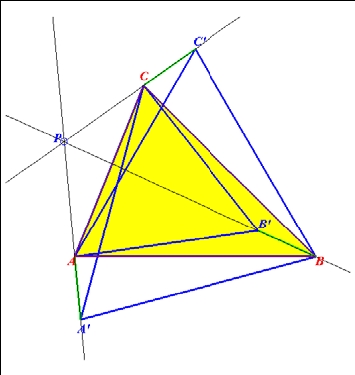
Låt ABC vara en godtycklig triangel där alla vinklar är mindre än 120o. Rita över varje triangelsida en liksidig triangel på utsidan av ABC med nya hörnpunkterna A’ , B’ , C’ .
a) Visa att linjerna genom AA’ , BB’ och CC’ skär varandra i en punkt P.
b) Visa att sträckorna AA’ , BB’ och CC’ är lika långa.
c) Visa att vinklarna mellan AP och PB, mellan BP och PC och mellan CP och PA är 120o.
d) Visa att P löser Fermat:s minimumproblem.
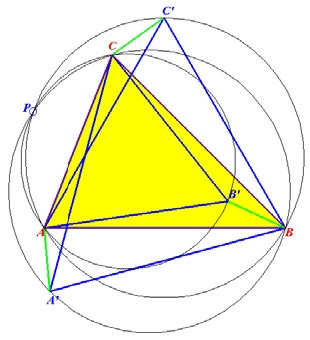
e) Visa att de till de liksidiga trianglarna AB’C, ABC’ och A’BC omskrivna cirklarna skär varandra i P.
ANMÄRKNING
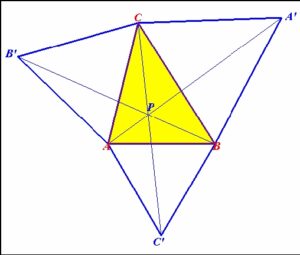
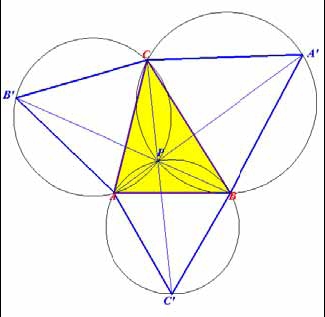
Den ovan konstruerade punkten kallas även ”första Fermatpunkten”; den ”andra Fermatpunkten” för man om man genomför samma konstruktion som ovan men med liksidiga trianglar ”inåt” triangeln:
|AA’ | = |BB’ | = |CC’ |, P är skärningspunkten mellan linjerna genom CC’ , AA’ och BB’ = skärningspunkten mellan de omskrivna cirklarna.