Handledning – Den Besvärliga Sänglådan

[latexpage]

Förkunskaper: Likformighet, (ev. ekvationssystem), grafisk/numerisk bestämning av funktionsmaximum/nollställe. Ma4.

Syfte: Lösa ett problem ur verkligheten, med en lättare del (bestäm ”x”) och en svårare (bestäm ”y”).

Lösningsförslag inkl. elevtips
Tips: rita figur, använd likformighet för att bestämma ”x”. Teckna ett uttryck för ”y” och sök ”y”-max. Använd grafräknare om nödvändigt.

Lösning: Notera att lådans botten tillsammans med väggen och golvet bildar en halv liksidig triangel. Likformiga trianglar markerade med minsta vinkeln = π/6.

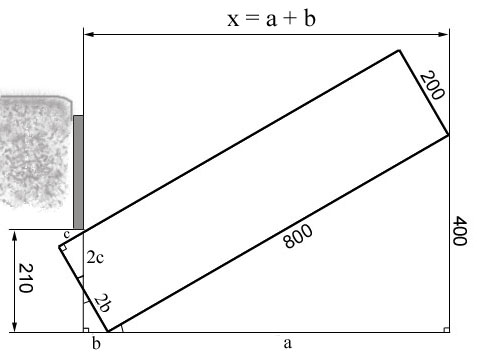
Sök x:

Metod I:
Beräkna avståndet ”x”: Två likformiga rätvinkliga trianglar under sängkanten ger ekvationssystemet: $$\left{\begin{array} 2b+\sqrt{3}c=200\ \sqrt{3}b+2c=210. \end{array}\right.$$ Vilket ger $$ 2\cdot(1)-\sqrt{3}\cdot(2)\ \Rightarrow \ b=400-210\sqrt{3}\text{ och } a=400\sqrt{3}$$

Svar: ”x” = ”a” + ”b” ≈ 729 mm.

Metod II:
Metod II använder två större likformiga rätvinkliga trianglar ovanför lådan: drag en vågrät linje genom lådans övre hörn. (på höjden ”h” = 400 + 100$ \sqrt{3} $) Den lodräta katetern över sänggaveln blir ”k1” = ”h” – 210 och den vågräta katetern ”k2” = ”k1”/tan (π/6). Avståndet ”x” ges sedan av ”k2” + 100 ≈ 729 mm. (lösning: Rolf Pettersson).

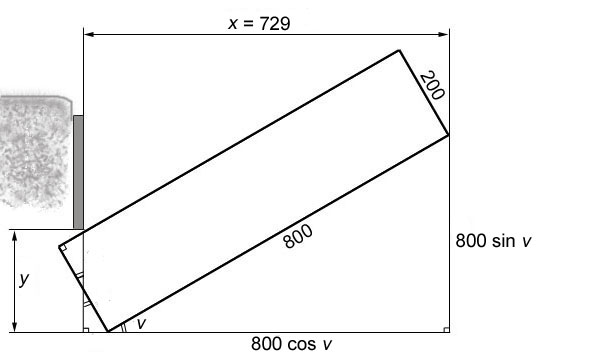
Sök y:

Metod I: Låt ”y” (mm) = lådans höjd över golvet vid sängsidans kant. Variabeln ”v” = lådans vinkel med golvet i radianer. 0 < ”v” < π/6. $ b = x-800\cdot cos(v) $

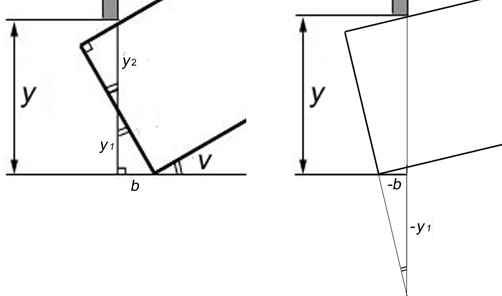
Observera att ”b” < 0 då ”v” < 0.4245 radianer (24.3°). $ y_{1}\cdot tan(v)=b $ $ y_{2}\cdot cos(v)=200-\frac{b}{sin(v)} $ $ y = y_{1} + y_{2} = \frac{b}{tan(v)}+\frac{200}{cos(v)}-\frac{b}{sin(v)\cdot cos(v)}= $ $ =\frac{x-800\cdot cos(v)}{tan(v)}+\frac{200}{cos(v)}-\frac{x-800\cdot cos(v)}{sin(v)\cdot cos(v)}= $ $ =\frac{800(1-cos^{2}(v))}{sin(v)}+\frac{200}{cos(v)}-\frac{x(1-cos^{2}(v))}{sin(v)\cdot cos(v)}= $ $ =800\cdot sin(v)+\frac{200}{cos(v)}-x\cdot tan(v) $.

Sambandet ”y” = ”y”’1’ + ”y”’2’ gäller för alla vinklar 0 < ”v” < π/6, även när ”b” och därmed ”y”’1’ är negativt. (se figur). Sök den vinkel som ger ”y”'(”v”) = 0. $ y'(v)=800\cdot cos(v)+\frac{200\cdot sin(v)}{cos^{2}(v)}-\frac{x}{cos^{2}(v)}=0\Leftrightarrow $ $ \Leftrightarrow 800\cdot cos^{3}(v)+200\cdot sin(v)-x=0 $. Numerisk lösning direkt på räknare, alt. med Newton-Raphsons metod ger ”v” = 0.355. ”y”(0.355) = 221 mm, sängen behöver lyftas minst 11 mm för att lådan ska kunna glida på plats.

Metod II: Alternativt väljer man variabeln ”h” (mm) = höjden över golvet i mm för lådans hörn vid väggen. 0 < ”h” < 400. $ b=x-\sqrt{800^{2}-h^{2}} $. Observera att ”b” < 0 då ”h” < 330. $\begin{array}{rl} y(h)&=\frac{200-800b/h}{cos(v)}+b\cdot cot(v)=\\ &=\frac{800(200-800\frac{x-\sqrt{640000-h^{2}}}{h})}{\sqrt{640000-h^{2}}}+(x-\sqrt{640000-h^{2}})\sqrt{640000/h^{2}-1} \end{array} $.

Grafisk bestämning av ”y”-max ger ”y” = 221 mm för ”h” = 278 mm.

Nästa steg: Vill du räkna mera på sänglådan? Bestäm i så fall det minsta avstånd mellan säng och vägg (”x”), där lådan glider på plats utan att man behöver lyfta sängen (”y”-max = 210).

Av Samuel Bengmark