Handledning – Ellipsens Ekvation

[latexpage]

Förkunskaper: Ma1, Algebra

Lösningsförslag inkl. elevtips

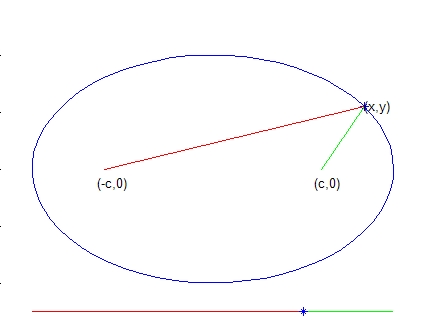
Om $ (x,y) $ är en punkt på ellipsen så gäller enligt avståndsformeln att $ \sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a$ med $ a>c $. Överflyttning och kvadrering ger $ (x-c)^2+y^2=4a^2+(x+c)^2+y^2-4a\sqrt{(x+c)^2+y^2} $ där förenkling ger att $ a\sqrt{(x+c)^2+y^2}=a^2+xc $. Ytterligare kvadrering ger att $ a^2(x^2+2xc+c^2+y^2)=a^4+2a^2xc+x^2c^2 $ dvs $ (a^2-c^2)x^2+a^2y^2=(a^2-c^2)a^2 $. Resultatet fås genom att sätta $ b^2=a^2-c^2 $.

En liten film som illustration:

Nästa steg:

Av Samuel Bengmark