Medianerna I En Triangel

Samuel Bengmark Uppgift 17 november, 2021 | 0

Uppgift

En triangel ABC är given. Vi tänker oss en följd, $T_0 ,\;T_1 ,\;T_2 ,\; \ldots$ av trianglar definierade på följande sätt

$T_0 =\triangle ABC=\triangle A_0B_0C_0$ $T_n =\triangle A_nB_nC_n$ ,där $A_n$ är mittpunkt på sidan $B_{n - 1}C_{n - 1}$ , $B_n$ är mittpunkt på sidan $A_{n - 1} C_{n - 1}$ $C_n$ är mittpunkt på sidan $B_{n - 1} A_{n - 1}$ .

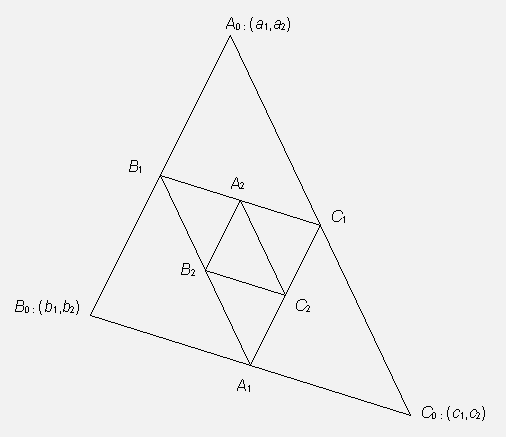
Bevisa att

medianerna till $T_0$ är medianer även till $T_n$ för alla n.

medianerna till $T_0$ har en gemensam skärningspunkt.

koordinaterna får dessa medianers skärningspunkt är $\left( {\frac{{a_1 + b_1 + c_1 }}{3},\frac{{a_2 + b_2 + c_2 }}{3}} \right)$ , där $\left( {a_1 ,a_2 } \right)$ är koordinaterna för A, $\left( {b_1 ,b_2 } \right)$ för B och $\left( {c_1 ,c_2 } \right)$ för C.

Medianerna I En Triangel

Medianerna I En Triangel

Uppgift

Kategori

Ämnesområde

Info

Material

Medverkande

MATTESHERPA