NAPOLEONTRIANGEL
Uppgift
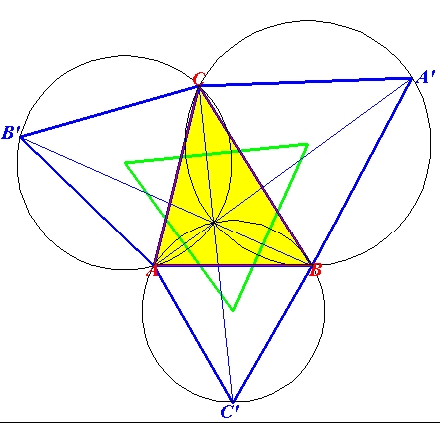
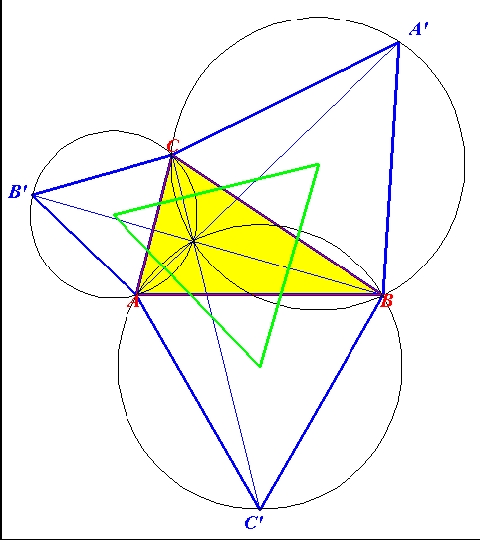
Låt ABC vara en godtycklig triangel där alla vinklar är mindre än 120o. Rita över varje triangelsida en liksidig triangel på utsidan av ABC med nya hörnpunkterna A’ , B’ , C’ .
Mittpunkterna till de till de tre trianglarna AB’C, ABC’ och A’BC omskrivna cirklarna är hörnpunkter i en liksidig triangel, den såkallada yttre Napoleon-triangeln, grön i figurerna:
TILLÄGG
1. Du kan även rita liksidiga trianglar ”inåt” triangeln ABC, mittpunktarna till deras omskrivna cirklar är hörnpunkter till en liksidig triangel, den såkallade ”inre” Napoleon-triangeln:
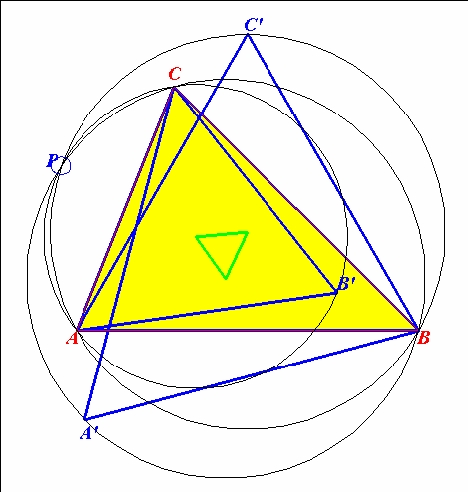
2. Beräkna längden av sidan av den inre resp. den yttre Napoleontriangeln och visa att den givna triangelns area är differensen mellan den yttre Napoleontriangelns area och den inre Napoleontriangelns area.