Cevias Sats

Samuel Bengmark Uppgift 17 november, 2021 | 0

Visa satsen av Ceva (Giovanni Ceva, 1684-1734):

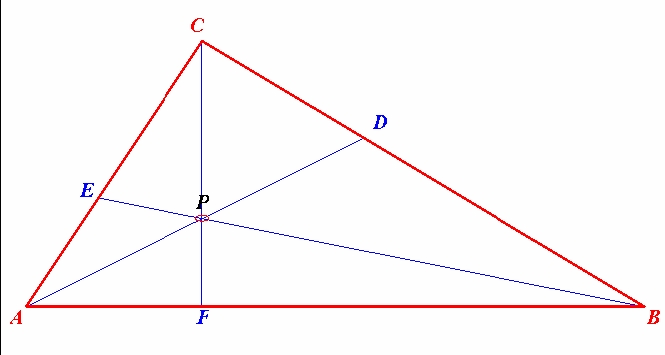
För en godtycklig triangel $ABC$ och punkter $D$ , $E$ och $F$ på triangelns sidor ( $D$ ligger på $BC$ , $E$ på $CA$ , $F$ på $AB$ ) gäller:

Sträckorna $AD$ , $BE$ och $CF$ skär varandra i en punkt om och endast om

$\begin{equation*}\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1.\end{equation*}$

TILLÄMPNING

Visa

a) Satserna att bisektriserna, höjderna och medianerna i en triangel skär varandra i en punkt.

b) Gergonnes sats (se Gergonnepunkten).

Info